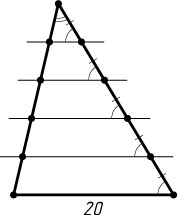
1500. Боковая сторона треугольника разделена на пять равных частей; через точки деления проведены прямые, параллельные основанию. Найдите отрезки этих прямых, заключённые между боковыми сторонами, если основание равно 20.
Ответ. 4, 8, 12, 16.
Указание. Каждая из указанных параллельных прямых отсекает от данного треугольника подобный ему треугольник.
Решение. Каждая из четырёх указанных прямых отсекает от данного треугольника подобный ему треугольник (признак подобия треугольников по двум углам). Коэффициенты подобия равны: \frac{1}{5}
, \frac{2}{5}
, \frac{3}{5}
и \frac{4}{5}
. Тогда соответствующие отрезки равны:
\frac{1}{5}\cdot20=4,~\frac{2}{5}\cdot20=8,~\frac{3}{5}\cdot20=12,~\frac{4}{5}\cdot20=16.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 9, с. 43
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.1, с. 111
