1506. На диагоналях AC
и BD
трапеции ABCD
взяты соответственно точки M
и N
так, что AM:MC=DN:NB=1:4
. Найдите MN
если основания AD=a
, BC=b
(a\gt b)
.
Ответ. \frac{4a-b}{5}
.
Указание. Продолжите MN
до пересечения с одной из боковых сторон трапеции.
Решение. Проведём через точку M
прямую, параллельную основаниям. Пусть K
и N_{1}
— её точки пересечения со стороной CD
и диагональю BD
соответственно. Из теоремы Фалеса следует, что
DK:KC=AM:MC=1:4,~DN_{1}:N_{1}B=DK:KC=1:4.
Поэтому точка N_{1}
совпадает с точкой N
. Следовательно, MN\parallel AD
.
Из подобия треугольников CKM
и CDA
находим, что
MK=\frac{4}{5}AD=\frac{4}{5}a,
а из подобия треугольников DKN
и DCB
—
KN=\frac{1}{5}BC=\frac{1}{5}b.
Следовательно,
MN=MK-KN=\frac{4a-b}{5}.
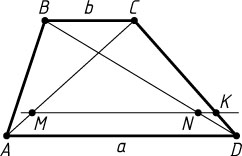
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.4, с. 111
