1510. На стороне BC
треугольника ABC
взята точка D
так, что \frac{BD}{CD}=\frac{AB}{AC}
. Докажите, что AD
— биссектриса треугольника ABC
.
Указание. Воспользуйтесь свойством биссектрисы треугольника.
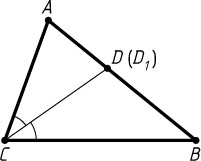
Решение. Проведём биссектрису AD_{1}
. Тогда BD_{1}:D_{1}C=AB:AC
.
Из единственности точки, делящей данный отрезок в данном отношении (считая от данного конца отрезка), следует, что точки D
и D_{1}
совпадают. Поэтому AD
— биссектриса треугольника ABC
.
Примечание. Аналогично, если для точки D
, лежащей на продолжении стороны BC
треугольника ABC
, верно равенство \frac{BD}{CD}=\frac{AB}{AC}
, то AD
— биссектриса внешнего угла при вершине A
треугольника.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 115
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 609, с. 155
