1511. Диагональ AC
трапеции ABCD
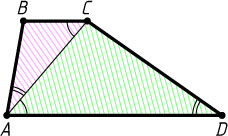
делит её на два подобных треугольника. Докажите, что AC^{2}=ab
, где a
и b
— основания трапеции.
Указание. Определите, какие стороны подобных треугольников соответствуют друг другу.
Решение. Пусть AD=a
, BC=b
. Поскольку \angle BCA=\angle CAD
, то сторона AB
соответствует стороне CD
. Тогда сторона BC
соответствует стороне AC
(иначе ABCD
— параллелограмм), а треугольник ABC
подобен треугольнику DCA
. Поэтому \frac{BC}{AC}=\frac{AC}{AD}
. Следовательно, AC^{2}=BC\cdot AD=ab
.
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 605, с. 154
