1512. Через точку пересечения диагоналей трапеции проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, заключённого внутри трапеции, если основания трапеции равны a
и b
.
Ответ. \frac{2ab}{a+b}
.
Указание. Рассмотрите две пары подобных треугольников.
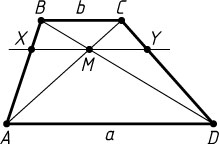
Решение. Пусть M
— точка пересечения диагоналей AC
и BD
трапеции ABCD
, X
и Y
— точки пересечения данной прямой с боковыми сторонами AB
и CD
. Из подобия треугольников BMC
и DMA
находим, что
\frac{AM}{MC}=\frac{AD}{BC}=\frac{a}{b}.
Поэтому \frac{AM}{AC}=\frac{a}{a+b}
.
Из подобия треугольников AMX
и ACB
находим, что
\frac{MX}{BC}=\frac{AM}{AC}=\frac{a}{a+b}.
Поэтому
MX=\frac{a\cdot BC}{a+b}=\frac{ab}{a+b}.
Аналогично находим, что MY=\frac{ab}{a+b}
. Следовательно,
XY=MX+MY=\frac{2ab}{a+b}.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 151, с. 16
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.275, с. 177
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 40, с. 10
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 40, с. 8
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 29, с. 170
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.13, с. 112
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 34, с. 11
