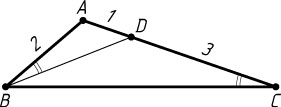
1517. В треугольнике ABC
проведена прямая BD
так, что \angle ABD=\angle BCA
. Найдите отрезки AD
и DC
, если AB=2
и AC=4
.
Ответ. 1 и 3.
Указание. Треугольники ABD
и ACB
подобны.
Решение. Треугольники ABD
и ACB
подобны по двум углам (\angle A
— общий, \angle ABD=\angle BCA
по условию). Поэтому \frac{AD}{AB}=\frac{AB}{AC}
. Следовательно,
AD=\frac{AB^{2}}{AC}=\frac{4}{4}=1,~CD=AC-AD=4-1=3.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 19, с. 46
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.8, с. 111
