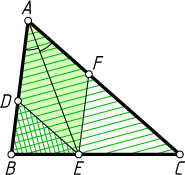
1518. В треугольник ABC
вписан ромб ADEF
так, что угол A
у них общий, а вершина E
находится на стороне BC
. Найдите сторону ромба, если AB=c
и AC=b
.
Ответ. \frac{bc}{b+c}
.
Указание. Диагональ ромба является биссектрисой его угла.
Решение. Пусть точка D
лежит на стороне AB
треугольника ABC
. Поскольку AE
— биссектриса угла A
, то
\frac{BE}{EC}=\frac{AB}{AC}=\frac{c}{b}.
Поэтому \frac{BE}{BC}=\frac{c}{b+c}
.
Из подобия треугольников BDE
и BAC
следует, что \frac{DE}{AC}=\frac{BE}{BC}
. Отсюда находим, что сторона ромба равна:
DE=\frac{AC\cdot BE}{BC}=\frac{bc}{b+c}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 32, с. 50
Источник: Вступительный экзамен в МИИТ. — 1979
