1519. Прямая, проведённая через вершину ромба вне его, отсекает на продолжении двух сторон отрезки p
и q
. Найдите сторону ромба.
Ответ. \sqrt{pq}
.
Указание. Рассмотрите подобные треугольники.
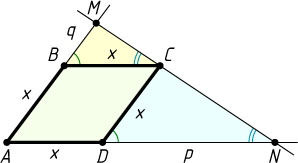
Решение. Обозначим через x
сторону ромба ABCD
. Пусть данная прямая проходит через точку C
и пересекает продолжения сторон AB
и AD
в точках M
и N
соответственно. Пусть BM=q
, DN=p
.
Из подобия треугольников MBC
и CDN
находим, что
\frac{BC}{DN}=\frac{BM}{CD},~\mbox{или}~\frac{x}{p}=\frac{q}{x}.
Следовательно, x=\sqrt{pq}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 33, с. 50
