1520. В треугольник с основанием a
и высотой h
вписан квадрат так, что две его вершины лежат на основании треугольника, а две другие — на боковых сторонах. Найдите сторону квадрата.
Ответ. \frac{ah}{a+h}
.
Указание. Используйте равенство отношений соответствующих высот к основаниям в подобных треугольниках.
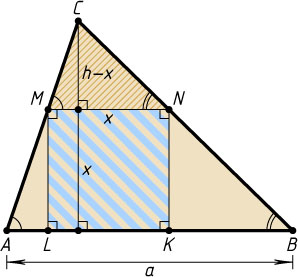
Решение. Пусть вершины M
и N
квадрата MNKL
находятся на боковых сторонах AC
и BC
треугольника ABC
, а вершины K
и L
— на основании AB
. Обозначим через x
сторону квадрата.
Высоты подобных треугольников MCN
и ACB
, проведённые из вершины C
, относятся как основания MN
и AB
, т. е.
\frac{h-x}{h}=\frac{x}{a}.
Отсюда находим, что x=\frac{ah}{a+h}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 36 с. 50
