1527. Дан треугольник ABC
. На продолжении стороны AC
за точку C
взята точка N
, причём CN=AC
; точка K
— середина стороны AB
. В каком отношении прямая KN
делит сторону BC
?
Ответ. 2:1
, считая от точки B
.
Указание. Медианы треугольника делятся точкой пересечения в отношении 2:1
, считая от вершины.
Решение. Первый способ. Пусть M
— точка пересечения прямых KN
и BC
. В треугольнике ABN
отрезки BC
и NK
— медианы. Поэтому BM:MC=2:1
.
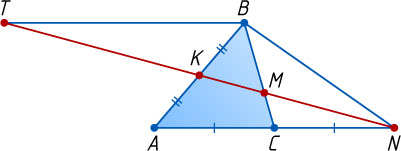
Второй способ. Пусть M
— точка пересечения прямых KN
и BC
. Через вершину B
проведём прямую, параллельную AC
, и продолжим NK
до пересечения с этой прямой в точке T
.
Треугольник BKT
равен треугольнику AKN
по стороне и двум прилежащим к ней углам, поэтому BT=AN
.
Треугольник BTM
подобен треугольнику CNM
по двум углам, значит,
\frac{BM}{MC}=\frac{BT}{CN}=\frac{AN}{CN}=\frac{2CN}{CN}=2.
