1535. На медиане AA_{1}
треугольника ABC
взята точка M
, причём AM:MA_{1}=1:3
. В каком отношении прямая BM
делит сторону AC
?
Ответ. 1:6
, считая от точки A
.
Указание. Через вершину B
проведите прямую, параллельную AC
.
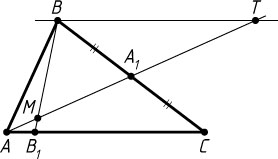
Решение. Проведём через точку B
прямую, параллельную AC
, и продолжим AA_{1}
до пересечения с этой прямой в точке T
. Пусть B_{1}
— точка пересечения прямой BM
со стороной AC
.
Из равенства треугольников BA_{1}T
и CA_{1}A
следует, что BT=AC
и TA_{1}=AA_{1}
. Поэтому TM:MA=7:1
. Из подобия треугольников AMB_{1}
и TMB
(коэффициент \frac{1}{7}
) следует, что
AB_{1}=\frac{1}{7}BT=\frac{1}{7}AC.
Следовательно,
B_{1}C=\frac{6}{7}AC,~AB_{1}:B_{1}C=1:6.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.8, с. 46
