1549. В равнобедренном треугольнике ABC
(AB=BC)
на стороне BC
взята точка D
так, что BD:DC=1:4
. В каком отношении прямая AD
делит высоту BE
треугольника ABC
, считая от вершины B
?
Ответ. 1:2
.
Указание. Продолжите AD
до пересечения с прямой, проходящей через вершину B
параллельно AC
.
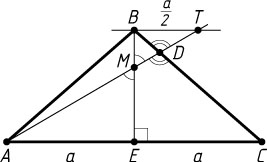
Решение. Пусть M
— точка пересечения AD
и BE
. Через точку B
проведём прямую, параллельную основанию AC
, и продолжим AD
до пересечения с этой прямой в точке T
. Пусть AE=a
. Тогда AC=2a
.
Из подобия треугольников BDT
и CDA
находим, что
BT=\frac{1}{4}AC=\frac{a}{2}.
Из подобия треугольников AME
и TMB
находим, что
\frac{BM}{ME}=\frac{BT}{AE}=\frac{1}{2}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.261, с. 176
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.7, с. 46
