1557. В треугольнике ABC
, все стороны которого различны, биссектриса угла BAC
пересекает сторону BC
в точке D
. Известно, что AB-BD=a
, AC+CD=b
. Найдите AD
.
Ответ. \sqrt{ab}
.
Указание. «Распрямите» ломаные ABD
и ACD
и рассмотрите образовавшиеся при этом подобные треугольники.
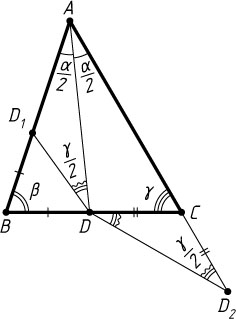
Решение. Отложим на луче BA
отрезок BD_{1}
, равный BD
, а на продолжении отрезка AC
за точку C
— отрезок CD_{2}
, равный CD
. Тогда AD_{1}=a
, AD_{2}=b
и треугольники D_{1}BD
и D_{2}CD
— равнобедренные.
Обозначим углы треугольника ABC
через \alpha
, \beta
и \gamma
соответственно. Докажем, что треугольники AD_{1}D
и ADD_{2}
подобны. Действительно,
\angle D_{1}AD=\angle DAD_{2}=\frac{\alpha}{2},
\angle ADD_{1}=\angle BD_{1}D-\angle BAD=90^{\circ}-\frac{\beta}{2}-\frac{\alpha}{2}=\frac{\gamma}{2},
\angle DD_{2}A=\frac{1}{2}\angle DCA=\frac{\gamma}{2}.
Отсюда следует подобие треугольников AD_{1}D
и ADD_{2}
. Следовательно,
\frac{AD_{1}}{AD}=\frac{AD}{AD_{2}}.
Отсюда находим, что AD^{2}=AD_{1}\cdot AD_{2}=ab
.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 157, с. 175
Источник: Вступительный экзамен на физический факультет МГУ. — 1976, № 4, вариант 1
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 229, с. 26
