1562. В треугольнике ABC
точки P
и Q
лежат на стороне AC
, а прямые BP
и BQ
делят медиану AM
на три равные части. Известно, что BP=BQ
, AB=9
, BC=11
. Найдите AC
.
Ответ. \frac{20}{\sqrt{3}}
.
Указание. Через вершину B
проведите прямую, параллельную AC
.
Решение. Обозначим AC=x
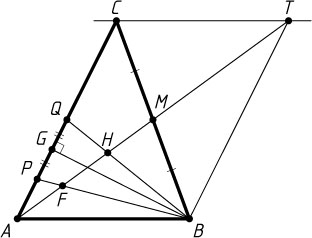
. Проведём через вершину B
прямую, параллельную AC
, и продолжим медиану AM
до пересечения с этой прямой в точке T
. Из равенства треугольников BMT
и CMA
следует, что BT=AC=x
, MT=AM
.
Пусть F
и H
— точки пересечения медианы AM
с отрезками BP
и BQ
соответственно. Тогда
AF=\frac{1}{6}AT,~AH=\frac{1}{3}AT.
Из подобия треугольников AFP
и TFB
следует, что
AP=\frac{1}{5}BT=\frac{x}{5},
а из подобия треугольников AHQ
и THB
—
AQ=\frac{1}{2}BT=\frac{x}{2}.
Тогда
PQ=AQ-AP=\frac{x}{2}-\frac{x}{5}=\frac{3x}{10}.
Проведём высоту BG
равнобедренного треугольника PQB
. Тогда G
— середина PQ
и
AG=AP+\frac{1}{2}PQ=\frac{x}{5}+\frac{3x}{20}=\frac{7x}{20},
CG=CQ+\frac{1}{2}PQ=\frac{13x}{20}.
Из прямоугольных треугольников AGB
и CGB
находим, что
BG^{2}=AB^{2}-AG^{2}=BC^{2}-CG^{2},~\mbox{или}~81-\left(\frac{7x}{20}\right)^{2}=121-\left(\frac{13x}{20}\right)^{2}.
Отсюда следует, что x=\frac{20}{\sqrt{3}}
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1985, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 154
