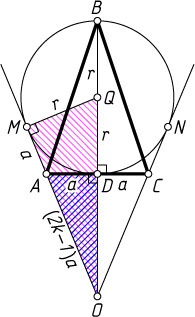
1593. В равнобедренном треугольнике ABC
(AB=BC)
на высоте BD
как на диаметре построена окружность. Через точки A
и C
к окружности проведены касательные AM
и CN
, продолжения которых пересекаются в точке O
. Найдите отношение \frac{AB}{AC}
, если \frac{OM}{AC}=k
и высота BD
больше основания AC
.
Ответ. \frac{1}{2}\sqrt{\frac{5k-1}{k-1}}
.
Указание. Рассмотрите подобные треугольники ODA
и OMQ
, где Q
— центр окружности.
Решение. Поскольку BD\gt AC
, то точки O
и B
лежат по разные стороны от прямой AC
. Пусть Q
— центр окружности. Обозначим AD=DC=a
, QD=r
. Тогда
AM=AD=a,~OM=kAC=2ak,
AO=OM-AM=2ak-a=(2k-1)a.
Из подобия треугольников ODA
и OMQ
находим, что \frac{OD}{AD}=\frac{OM}{QM}
. Поэтому
OD=\frac{OM\cdot AD}{QM}=\frac{2ka\cdot a}{r}=\frac{2ka^{2}}{r}.
По теореме Пифагора
AO^{2}=AD^{2}+OD^{2},~\mbox{или}~(2k-1)^{2}a^{2}=a^{2}+\frac{4k^{2}a^{2}}{r^{2}}.
Отсюда находим, что r^{2}=\frac{a^{2}k}{k-1}
. Тогда
AB=\sqrt{BD^{2}+AD^{2}}=\sqrt{4r^{2}+a^{2}}=
=\sqrt{\frac{4a^{2}k}{k-1}+a^{2}}=a\sqrt{\frac{5k-1}{k-1}}.
Следовательно, \frac{AB}{AC}=\frac{1}{2}\sqrt{\frac{5k-1}{k-1}}
.
Источник: Вступительный экзамен в МФТИ. — 1972, № 3, билет 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 72-3-3, с. 153
