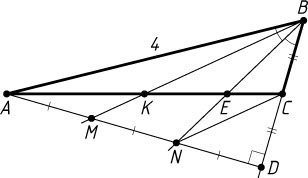
1598. В треугольнике ABC
проведены: BK
— медиана, BE
— биссектриса, AD
— высота. Найдите сторону AC
, если известно, что прямые BK
и BE
делят отрезок AD
на три равные части и AB=4
.
Ответ. \sqrt{13}
.
Решение. Пусть M
и N
— точки пересечения прямых BK
и BE
с отрезком AD
, AM=MN=ND
. Заметим, что точка N
не может лежать между A
и M
, так как тогда по свойству биссектрисы в прямоугольном треугольнике ABD
стороны AB
и BD
пропорциональны отрезкам AN
и DN
, т. е. BD=2AB
, т. е. гипотенуза меньше катета, что невозможно. Следовательно, точка N
лежит между D
и M
. Тогда
BD=\frac{1}{2}AB=2,~AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{16-4}=2\sqrt{3},
Поскольку M
— середина AN
, а K
— середина AC
, отрезок MK
— средняя линия треугольника ACN
, значит, MK\parallel CN
, а так как N
— середина DM
и CN\parallel BM
, то CM
— средняя линия треугольника DBM
. Следовательно, C
— середина BD
. Тогда CD=\frac{1}{2}BD=1
и из прямоугольного треугольника ACD
находим, что
AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{12+1}=\sqrt{13}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 87, с. 14
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 87, с. 12
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 130, с. 201
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.20, с. 47
