1600. В треугольнике ABC
высота BD
равна 6, медиана CE
равна 5, расстояние от точки пересечения отрезков BD
и CE
до стороны AC
равно 1. Найдите сторону AB
.
Ответ. \frac{2\sqrt{145}}{3}
.
Указание. Продолжите медиану CE
до пересечения с прямой, проходящей через вершину B
параллельно AC
, и рассмотрите образовавшиеся подобные треугольники.
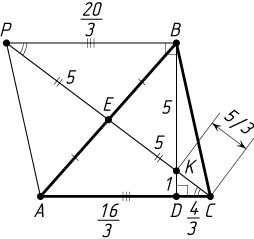
Решение. Пусть K
— точка пересечения отрезков BD
и CE
, P
— точка пересечения прямой CE
с прямой, проведённой через вершину B
параллельно AC
. Из равенства треугольников PBE
и CAE
следует, что BP=AC
, а из подобия треугольников PKB
и CKD
—
DC=\frac{1}{5}BP=\frac{1}{5}AC,~KC=\frac{1}{6}CP=\frac{1}{6}\cdot10=\frac{5}{3}.
Из прямоугольного треугольника KDC
находим, что
DC=\sqrt{KC^{2}-KD^{2}}=\sqrt{\left(\frac{5}{3}\right)^{2}-1}=\frac{4}{3}.
Поэтому
AC=BP=5DC=\frac{20}{3},~AD=\frac{4}{5}AC=\frac{16}{3}.
Из прямоугольного треугольника ADB
находим, что
AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{\left(\frac{16}{3}\right)^{2}+6^{2}}=\sqrt{\frac{580}{9}}=\frac{2\sqrt{145}}{3}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1982, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 72
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2.18.1, с. 20
