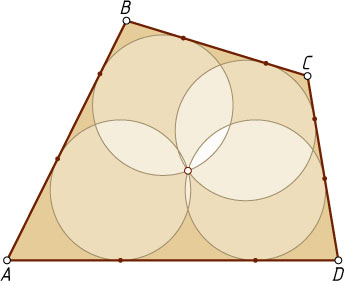
16015. Четыре равных окружности проходят через одну точку, а каждая сторона четырёхугольника ABCD
касается двух из этих окружностей (см. рис.). Докажите, что четырёхугольник ABCD
вписанный.
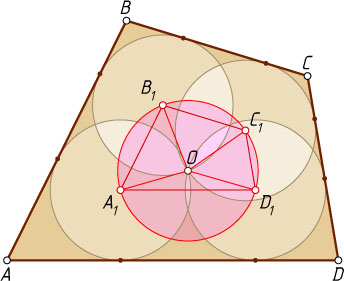
Решение. Пусть A_{1}
, B_{1}
, C_{1}
и D_{1}
— центры данных окружностей радиуса R
, O
— общая точка окружностей. Поскольку окружности равные,
OA_{1}=OB_{1}=OC_{1}=OD_{1}=R.
Значит, точки A_{1}
, B_{1}
, C_{1}
и D_{1}
лежат на окружности с центром O
и радиусом R
, т. е. четырёхугольник A_{1}B_{1}C_{1}D_{1}
вписанный, и сумма его противоположных углов равна 180^{\circ}
. Его стороны соответственно параллельны сторонам четырёхугольника ABCD
, поэтому углы четырёхугольников соответственно равны. Значит, сумма противоположных углов четырёхугольника ABCD
, тоже равна 180^{\circ}
. Следовательно, он вписанный. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1983, № 7, задача 759 (1982, с. 174), с. 221

