16029. Даны два тупоугольных треугольника. Стороны первого равны a
, b
и c
, а второго — p
, q
и r
, причём c
и r
соответственно — их наибольшие стороны. Докажите, что ap+bq\lt cr
.
Решение. Пусть AB=c
— наибольшая сторона тупоугольного треугольника ABC
, а PQ=r
— наибольшая сторона треугольника PQR
. Предположим, что c\lt r
.
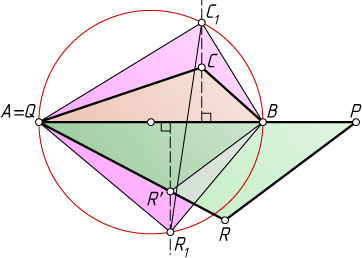
Расположим треугольники, как показано на рисунке: совместим вершины A
и Q
, отложим сторону AB
на стороне QP
, а вершины C
и R
поместим по разные стороны от прямой AP
.
Пусть прямая, проведённая через через точку B
параллельно RP
, пересекает AR
в точке R'
. Построим на отрезке AB
как на диаметре окружность. Поскольку углы данных треугольников при вершинах C
и R'
тупые, эти точки окажутся внутри окружности.
Через точки C
и R'
перпендикулярно диаметру AB
проведём прямые. Пусть первая из них пересекает окружность в точке C_{1}
, лежащей с точкой C
по одну сторону от AB
, а вторая — в точке R_{1}
, лежащей по другую сторону от AB
. Тогда
AB\geqslant C_{1}R_{1},~AC_{1}\gt AC,~BR_{1}\gt BR',~C_{1}B\gt CB,~R_{1}A\gt R'A.
Применив теорему Птолемея к вписанному четырёхугольнику AC_{1}BR_{1}
, получим
AB^{2}\geqslant AB\cdot C_{1}R_{1}=AC_{1}\cdot BR_{1}+C_{1}B\cdot R_{1}A\gt
\gt AC\cdot BR'+CB\cdot R'A.
Треугольники PQR
и BAR'
подобны, поэтому
\frac{BR'}{RP}=\frac{R'A}{QR}=\frac{AB}{PQ},
откуда
BR'=RP\cdot\frac{AB}{PQ},~R'A=QR\cdot\frac{AB}{PQ}.
Тогда
AB^{2}\gt AC\cdot RP\cdot\frac{AB}{PQ}+CB\cdot QR\cdot\frac{AB}{PQ}.
Умножив обе части этого неравенства на \frac{PQ}{AB}
, получим
AB\cdot PQ\gt AC\cdot RP+CB\cdot QR,~\mbox{или}~cr\gt bq+ap.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1986, № 7, задача 1030 (1985, с. 83), с. 193
