16077. Точка P
лежит на описанной окружности треугольника ABC
. Точки D
и E
— проекции точки P
на прямые BC
и CA
соответственно, L
и M
— середины отрезков AD
и BE
соответственно. Докажите, что DE\perp LM
.
Решение. Рассмотрим случай, изображённый на рисунке.
Поскольку
\angle CAP=\angle CBP~\mbox{и}~\angle AEP=\angle BDP~(=90^{\circ}),
треугольник AEP
подобен треугольнику BDP
, поэтому \frac{AE}{BD}=\frac{EP}{PD}
.
Пусть N
— середина стороны AB
. По теореме о средней линии треугольника
NL\parallel BD,~NM\parallel AE,~NL=\frac{1}{2}BD,~NM=\frac{1}{2}AE.
Тогда
\frac{NM}{NL}=\frac{\frac{1}{2}AE}{\frac{1}{2}BD}=\frac{AE}{BD}=\frac{EP}{PD},
а так как EP\perp AE
и DP\perp BD
, то EP\perp NM
и DP\perp NL
. Кроме того, \angle LNM=\angle DPE
как углы с соответственно перпендикулярными сторонами, поэтому треугольники NLM
и PDE
подобны. Следовательно, их третьи стороны LM
и DE
тоже перпендикулярны. Что и требовалось доказать.
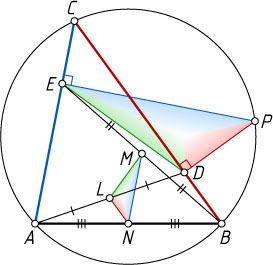
Источник: Журнал «Crux Mathematicorum». — 1993, № 9, задача 1799 (1992, с. 305), с. 271
