16081. Точки E
и F
расположены на сторонах соответственно BC
и AD
четырёхугольника ABCD
. Отрезки AE
и BF
пересекаются в точке P
, а отрезки CF
и DE
— в точке Q
. Докажите, что точки E
и F
делят BC
и AD
(или BC
и DA
) в одном и том же отношении тогда и только тогда, когда \frac{S_{\triangle FPQ}}{S_{\triangle EDA}}=\frac{S_{\triangle EQP}}{S_{\triangle FBC}}
.
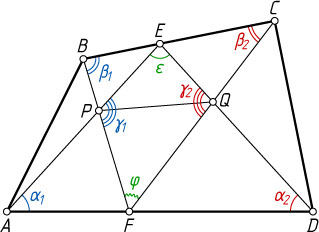
Решение. Рассмотрим случай, изображённый на рисунке.
Обозначим
\angle EAD=\alpha_{1},~\angle EDA=\alpha_{2},~\angle FBC=\beta_{1},~\angle FCB=\beta_{2},
\angle EPF=\gamma_{1},~\angle EQF=\gamma_{2}.
По теореме синусов
FP=\frac{AF\sin\alpha_{1}}{\sin\gamma_{1}},~FQ=\frac{FD\sin\alpha_{2}}{\sin\gamma_{2}},~EP=\frac{EB\sin\beta_{1}}{\sin\gamma_{1}},~EQ=\frac{EC\sin\beta_{2}}{\sin\gamma_{2}}.
Обозначим
\angle PFQ=\varphi,~\angle PEQ=\epsilon.
Тогда, учитывая, что по теореме синусов
\frac{ED}{\sin\alpha_{1}}=\frac{AD}{\sin\epsilon}=\frac{EA}{\sin\alpha_{2}},~\frac{FB}{\sin\beta_{2}}=\frac{BC}{\sin\varphi}=\frac{FC}{\sin\beta_{1}},
получим
\frac{S_{\triangle FPQ}}{S_{\triangle EDA}}=\frac{S_{\triangle EQP}}{S_{\triangle FBC}}~\Leftrightarrow~\frac{FP\cdot FQ\sin\varphi}{ED\cdot EA\sin\epsilon}=\frac{EP\cdot EQ\sin\epsilon}{FB\cdot FC\sin\varphi}~\Leftrightarrow
\Leftrightarrow~\frac{\frac{AF\sin\alpha_{1}}{\sin\gamma_{1}}\cdot\frac{FD\sin\alpha_{2}}{\sin\gamma_{2}}\cdot\sin\varphi}{\frac{AD\sin\alpha_{1}}{\sin\epsilon}\cdot\frac{AD\sin\alpha_{2}}{\sin\epsilon}\cdot\sin\epsilon}=\frac{\frac{EB\sin\beta_{1}}{\sin\gamma_{1}}\cdot\frac{EC\sin\beta_{2}}{\sin\gamma_{2}}\cdot\sin\epsilon}{\frac{BC\sin\beta_{2}}{\sin\varphi}\cdot\frac{BC\sin\beta_{1}}{\sin\varphi}\cdot\sin\varphi}~\Leftrightarrow
\Leftrightarrow~\frac{AF}{AD}\cdot\frac{FD}{AD}=\frac{BE}{BC}\cdot\frac{EC}{BC}~\Leftrightarrow~\frac{AF}{AD}\cdot\frac{AD-AF}{AD}=\frac{BE}{BC}\cdot\frac{BC-BE}{BC}~\Leftrightarrow
\Leftrightarrow~\frac{AF}{AD}\left(1-\frac{AF}{AD}\right)=\frac{BE}{BC}\left(1-\frac{BE}{BC}\right).
Пусть \frac{AF}{AD}=\lambda
, \frac{BE}{BC}=\mu
. Тогда последнее равенство примет вид
\lambda(1-\lambda)=\mu(1-\mu),~\mbox{или}~(\mu-\lambda)(\mu+\lambda-1)=0,
что выполняется тогда и только тогда, когда
\mu=\lambda~\mbox{или}~\mu=1-\lambda,
т. е.
\frac{AF}{AD}=\frac{BE}{BC}~\mbox{или}~\frac{AF}{AD}=\frac{CE}{BC}.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1994, № 3, задача 1833, с. 81
