16096. Во вписанный четырёхугольник ABCD
вписана окружность с центром I
. Прямая, проведённая через точку I
параллельно AB
, пересекает стороны AD
и BC
в точках A'
и B'
соответственно. Докажите, что отрезок A'B'
равен четверти периметра четырёхугольника ABCD
.
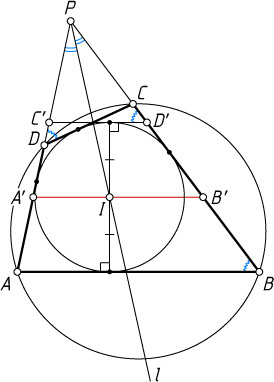
Решение. Рассмотрим случай, изображённый на рисунке. Пусть прямые AD
и BC
пересекаются в точке P
. Проведём биссектрису l
угла APB
(если AB\parallel CD
, то проведём через точку I
прямую l
, параллельную AB
и CD
).
Пусть точки C'
и D'
симметричны точкам соответственно C
и D
относительно прямой l
. Поскольку четырёхугольник ABCD
вписанный,
\angle ABC=\angle CDC'=\angle C'D'C,
поэтому C'D'\parallel AB
. Значит ABD'C'
— трапеция (или параллелограмм).
Из симметрии C'D'
касается вписанной окружности четырёхугольника ABCD
, значит, эта окружность вписана и в трапецию ABD'C'
, а также C'D'=CD
.
Поскольку точка I
— середина диаметра, перпендикулярного основаниям трапеции ABD'C'
, то по теореме Фалеса A'B'
— средняя линия описанной трапеции ABD'C'
, а так как четырёхугольник ABCD
описанный, то
AB+CD=AD+BC.
Значит,
A'B'=\frac{1}{2}(AB+C'D')=\frac{1}{2}(AB+CD)=\frac{1}{2}\cdot\left(\frac{1}{2}(AB+CD+AD+BC)\right)=
=\frac{1}{4}(AB+CD+AD+BC).
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1995, № 7, задача 1983 (1994, с. 250), с. 257
