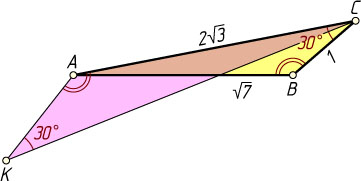
1610. В треугольнике ABC
известно, что AC=2\sqrt{3}
, AB=\sqrt{7}
, BC=1
. Вне треугольника взята точка K
так, что отрезок KC
пересекает отрезок AB
в точке, отличной от B
, и треугольник с вершинами K
, A
и C
подобен исходному. Найдите угол AKC
, если известно, что угол KAC
— тупой.
Ответ. 30^{\circ}
.
Указание. Докажите, что \angle AKC=\angle ACB
.
Решение. AC
— наибольшая сторона треугольника ABC
, а так как в треугольнике AKC
есть тупой угол, то это ABC
. Следовательно, угол ACB
треугольника ABC
не равен углу KAC
треугольника AKC
. Он также не равен углу KCA
, так как меньше его (луч CK
проходит между лучами CA
и CB
). Следовательно, \angle AKC=\angle ACB
.
По теореме косинусов из треугольника ABC
находим, что
\cos\angle ACB=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{12+1-7}{4\sqrt{3}}=\frac{6}{4\sqrt{3}}=\frac{\sqrt{3}}{2}.
Следовательно, \angle AKC=\angle ACB=30^{\circ}
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1969, № 3, вариант 3
