16119. Точки A
и B
лежат на диаметре MN
полуокружности. Точки C
, D
, E
и F
, лежащие на полуокружности, выбраны так, что \angle CAM=\angle EAN=\angle DBM=\angle FBN
. Докажите, что CE=DF
.
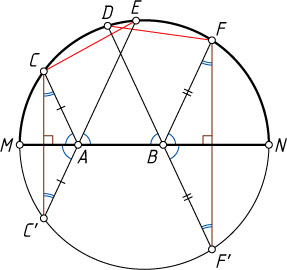
Решение. Рассмотрим случай, изображённый на рисунке.
Достроим данную полуокружность до окружности, и продолжим EA
и DB
до пересечения с окружностью в точках C'
и F'
соответственно. Поскольку окружность симметрична относительно любого своего диаметра (см. задачу 1677), а \angle C'AM=\angle CAM
, то точка A
лежит на отрезке EC'
. Аналогично, точка B
лежит на отрезке DF'
. Также AC=AC'
, поэтому \angle AC'C=\angle ACC'
и \angle BF'F=\angle BFF'
.
Тогда
2\angle EC'C=180^{\circ}-\angle CAC'=180^{\circ}-2\angle CAM=
=180^{\circ}-2\angle FBN=180^{\circ}-\angle FBF'=2\angle DF'F.
Значит, вписанные углы EC'C
и DF'F
равны. Следовательно, равны хорды, на которые опираются эти углы, т. е. CD=EF
. Что и требовалось доказать.
Источник: Канадские математические олимпиады. — 1997
Источник: Журнал «Crux Mathematicorum». — 1997, № 8, задача 3, с. 480
