16137. Медианы BM
и CN
треугольника ABC
пересекаются в точке G
. Описанные окружности \Gamma_{1}
и \Gamma_{2}
треугольников ANC
и AMB
вторично пересекаются в точке P
, а луч AP
пересекает описанную окружность треугольника AMN
в точке T
.
а) Найдите отношение AT:AP
.
б) Докажите, что \angle BAG=\angle CAT
.
Ответ. а) 2:3
.
Решение. а) Пусть при инверсии относительно окружности с центром A
произвольного радиуса R
точки C
, M
, B
, N
и P
переходят в точки C'
, M'
, B'
, N'
и P'
соответственно. Поскольку
2AM\cdot AC'=AC\cdot AC'=R^{2}=AM\cdot AM'~\Rightarrow~2AC'=AM',
точка C'
— середина отрезка AM'
. Аналогично, точка B'
— середина отрезка AN'
.
Прямая AP
проходит через центр инверсии, поэтому она переходит в себя. Окружность \Gamma_{2}
переходит в прямую B'M'
, окружность \gamma_{1}
— в прямую C'N'
. Значит, точка P
пересечения окружностей \Gamma_{1}
и \Gamma_{2}
— в точку P'
, и это точка пересечения прямых M'B'
и N'C'
, т. е. точка пересечения медиан треугольника AM'N'
.
Точка T
переходит в точку T'
пересечения AP'
и M'N'
, т. е. в середину отрезка M'N'
. Тогда
AT\cdot AT'=AP\cdot AP'=R^{2}~\Rightarrow~\frac{AT}{AP}=\frac{AP'}{AT'}=\frac{2}{3}.
б) Из подобия треугольников ABC
, ANM
и AM'N'
получаем
\angle CAT=\angle C'AT'=\angle M'AP'=\angle BAG.
Что и требовалось доказать.
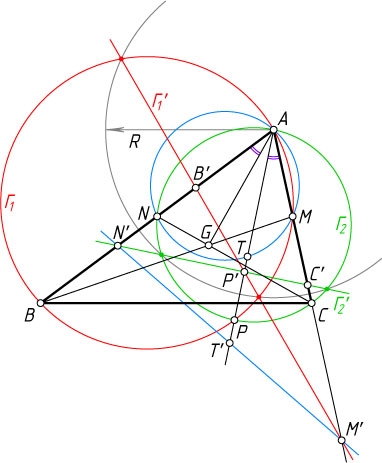
Источник: Журнал «Crux Mathematicorum». — 1999, № 4, задача 2349 (1998, с. 236), с. 255
