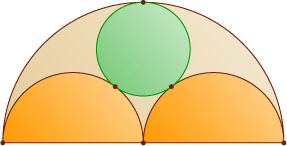
16138. Полуокружности радиуса 3 вписаны в полуокружность радиуса 6 (см. рис.). Найдите радиус окружности, касающейся всех трёх полуокружностей.
Ответ. 2.
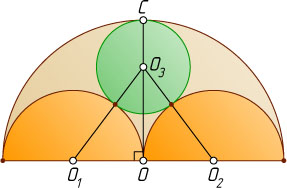
Решение. Пусть AB=12
— диаметр данной полуокружности с центром O
, O_{1}
и O_{2}
— центры данных полуокружностей радиуса 3, O_{3}
— центр окружности искомого радиуса r
, касающейся всех трёх данных полуокружностей, C
— точка касания данной полуокружности радиуса 6 с искомой окружностью. Тогда из симметрии O_{3}O
— высота равнобедренного треугольника O_{1}O_{2}O_{2}
со сторонами
O_{1}O_{2}=3+3=6,~O_{1}O_{3}=O_{2}O_{3}=3+r
и высотой
O_{3}O=CO-O_{3}C=6-r.
Из прямоугольного треугольника O_{3}OO_{1}
получаем, что
O_{3}O=\sqrt{O_{1}O_{3}^{2}-OO_{1}^{2}}=\sqrt{(r+3)^{2}-3^{2}}=\sqrt{r^{2}+6r}
Из уравнения
\sqrt{r^{2}+6r}=6-r
находим, что r=2
.
Источник: Журнал «Crux Mathematicorum». — 1999, № 5, задача 6, с. 285

