16169. Найдите
\ctg\frac{\pi}{7}+\ctg\frac{2\pi}{7}-\ctg\frac{3\pi}{7}.
Ответ. \sqrt{7}
.
Решение. Обозначим искомую сумму через S
. Пусть \frac{\pi}{7}=\alpha
, а точки A
, B
, C
, D
и E
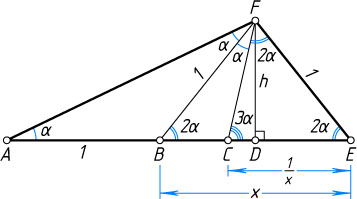
последовательно расположены на стороне AE
треугольника AFE
, причём
\angle BAF=\alpha,~AB=BF=FE=1,~CE=CF,~FD\perp AE.
Обозначим BE=x
. Тогда (см. рис.) из равнобедренного треугольника BFE
получаем
BD=DE=\frac{x}{2}.
Поскольку
\angle FBE=\angle FEB=\angle CFE=2\alpha,
треугольники FBE
и CFE
с общим углом при вершине E
подобны по двум углам. По теореме о внешнем угле треугольника \angle FCE=3\alpha
, а равнобедренные треугольники ECF
и EFB
тоже подобны по двум углам, то
CE=\frac{CE}{FE}=\frac{FE}{BE}=\frac{1}{x}~\Rightarrow~CD=CE-DE=\frac{1}{x}-\frac{x}{2}.
Пусть FD=h
. Тогда по теореме Пифагора
1-\frac{x^{2}}{2}=h^{2},
а
S=\ctg\alpha+\ctg2\alpha-\ctg3\alpha=\frac{AD}{h}+\frac{DE}{h}-\frac{CD}{h}~\Rightarrow~
Sh=AD+DE-CD=\left(1+\frac{x}{2}\right)+\frac{x}{2}-\left(\frac{1}{x}-\frac{x}{2}\right)=1+\frac{3}{2}x-\frac{1}{x}.
Треугольники FBC
и AEF
подобны по двум углам, поэтому
BC=\frac{BC}{BF}=\frac{EF}{EA}=\frac{1}{EA}=\frac{1}{x}.
Значит,
x=BE=BC+CE=\frac{1}{1+x}+\frac{1}{x}=\frac{2x+1}{x(x+1)}~\Rightarrow~
~\Rightarrow~\frac{1}{x}=x^{2}+x-2~\mbox{и}~x^{3}=-x^{2}+2x+1~\mbox{и}~x^{4}=-x^{3}+2x^{2}+x.
Тогда
4h^{2}S^{2}=4\left(1+\frac{3}{2}x-\frac{1}{x}\right)^{2}=4\left(1+\frac{3}{2}x-x^{2}-x+2\right)^{2}=
=(6+x-2x^{2})^{2}=36+12x-23x^{2}-4x^{3}+4x^{4}=
=36+12x-23x^{2}-4x^{3}+4(-x^{3}+2x^{2}+x)=
=36+16x-15x^{2}-8x^{3}=36+16x-15x^{2}-8(-x^{2}+2x+1)=
=28-7x^{2}=28\left(1-\frac{x^{2}}{4}\right)=28h^{2}.
Следовательно, S=\sqrt{7}
.