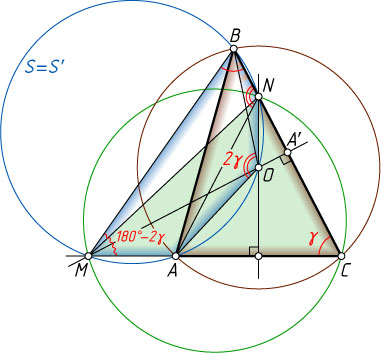
16173. Серединный перпендикуляр к стороне BC
непрямоугольного треугольника ABC
пересекает прямую AC
в точке M
, а серединный перпендикуляр к стороне AC
пересекает прямую BC
в точке N
. Точка O
— центр описанной окружности треугольника ABC
. Докажите, что:
а) точки A
, B
, M
, N
и O
лежат на одной окружности;
б) радиус этой окружности равен радиусу описанной окружности треугольника MNC
.
Решение. Обозначим \angle ACB=\gamma
. Пусть \gamma\lt90^{\circ}
. Рассмотрим случай, изображённый на рисунке.
а) Точка M
лежит на серединном перпендикуляре к отрезку BC
, поэтому MB=MC
. Тогда
\angle CMB=180^{\circ}-2\gamma.
Центральный угол AOB
описанной окружности треугольника ABC
вдвое больше соответствующего вписанного угла ACB
, т. е. \angle AOB=2\gamma
. Значит,
\angle CMB+\angle AOB=180^{\circ},
и поэтому четырёхугольник AMBO
вписан в некоторую окружность S
.
Точка N
лежит на серединном перпендикуляре к отрезку AC
, поэтому NA=NC
. Тогда по теореме о внешнем угле треугольника
\angle ANB=2\gamma=\angle AOB.
Значит, точки A
, B
, N
и O
лежат на некоторой окружности S'
, а так как через точки A
, B
и O
, не лежащие на одной прямой, проходит единственная окружность, окружность S'
совпадает с S
. Следовательно, точки A
, B
, M
, N
и O
лежат на одной окружности. Утверждение пункта а) доказано.
Для остальных случаев доказательство несущественно отличается от приведённого.
б) Четырёхугольник AMBN
вписан в окружность S
, поэтому
\angle CAB=180^{\circ}-\angle MAB=180^{\circ}-\angle MNB=\angle CNM.
Значит, треугольники MNC
и ABC
с общим углом при вершине C
подобны по двум углам. Тогда
\frac{MN}{AB}=\frac{CM}{BC}=\frac{CM}{2CA'},
где A'
— середина стороны BC
.
Из прямоугольного треугольника CA'M
получаем
CA'=CM\cos\angle MCA'=CM\cos\gamma~\Rightarrow~\frac{MN}{AB}=\frac{CM}{2CA'}=\frac{CM}{2CM\cos\gamma}=\frac{1}{2\cos\gamma}.
Значит, отношение радиусов R_{1}
и R
описанных окружностей подобных треугольников соответственно MNC
и ABC
равно коэффициенту подобия, т. е. \frac{1}{2\cos\gamma}
. Следовательно,
R_{1}=R\cdot\frac{1}{2\cos\gamma}=\frac{\frac{c}{2\sin\gamma}}{2\cos\gamma}=\frac{c}{2\sin2\gamma}=\frac{AB}{2\sin\angle ANB}.
Последняя величина равна радиусу описанной окружности треугольника ANB
, т. е. радиусу окружности S
. Утверждение пункта б) доказано.
Для \gamma\gt90^{\circ}
доказательство несущественно отличается от приведённого.
Источник: Молдавские математические олимпиады. — 1996
Источник: Журнал «Crux Mathematicorum». — 2001, № 6, задача 7, с. 368
