16174. Дан выпуклый пятиугольник ABCDE
, причём ACDE
— квадрат, а
\ctg\angle BDE+\ctg\angle DEB+\ctg\angle EBD=2.
Докажите, что треугольник ABC
прямоугольный.
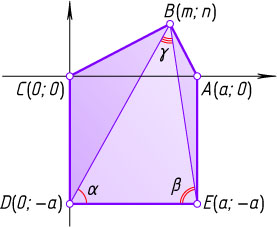
Решение. Введём прямоугольную систему координат так, чтобы вершины данного пятиугольника имели следующие координаты:
A(a;0),~B(m;n),~C(0;0),~D(0;-a),~E(a;-a).
Обозначим
\angle BDE=\alpha,~\angle DEB=\gamma,~\angle EBD=\beta.
Тогда
2=\ctg\alpha+\ctg\beta+\ctg\gamma=\frac{BD^{2}+DE^{2}+EB^{2}}{4S_{\triangle BDE}}
(см. задачу 3248а), т. е.
\frac{(m^{2}+(n+a)^{2})+a^{2}+((m-a)^{2}+(n+a)^{2})}{4\cdot\frac{1}{2}a(a+n)}=\frac{2m^{2}-2ma+2n^{2}+4an+4a^{2}}{2a(a+n)}=
=\frac{2m^{2}-2ma+2n^{2}}{2a(a+n)}+2=2.
Значит,
\frac{2m^{2}-2ma+2n^{2}}{2a(a+n)}=0~\mbox{или}~2m^{2}-2ma+2n^{2}=0,
откуда
(m^{2}+n^{2})+(m-a)^{2}+n^{2}-a^{2}=0,~\mbox{или}~(m^{2}+n^{2})+((m-a)^{2}+n^{2})=a^{2},
т. е.
BC^{2}+BA^{2}=CA^{2}.
Следовательно, \angle ABC=90^{\circ}
, и треугольник ABC
прямоугольный. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2001, № 6, задача H276, с. 398
