16187. Через точку A
, лежащую вне окружности \Gamma
, проведены прямые, касающиеся окружности в точках B
и C
. Произвольная касательная к окружности \Gamma
пересекает отрезки AB
и AC
в точках P
и Q
соответственно. Прямая, проходящая через точку P
параллельно AC
, пересекает BC
в точке R
. Докажите, что все прямые QR
проходят через фиксированную точку.
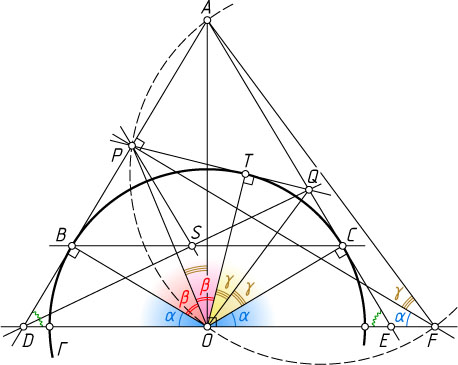
Решение. Пусть O
— центр окружности, а продолжение диаметра окружности \Gamma
, перпендикулярного AO
, пересекает прямые AB
и AC
в точках D
и E
соответственно. Докажем, что все прямые QR
проходят через точку D
. Для этого предположим, что прямая DQ
пересекает BC
в точке S
, и докажем, что PS\parallel AC
. Отсюда получим, что точка S
совпадает с R
.
Рассмотрим случай, изображённый на рисунке. Пусть прямая PQ
касается окружности \Gamma
в точке T
. Обозначим
\angle BOD=\angle EOC=\alpha,~\angle POB=\angle TOP=\beta,~\angle COQ=\angle QOT=\gamma.
Тогда
2\alpha+2\beta+2\gamma=180^{\circ}~\Rightarrow~\alpha+\beta+\gamma=90^{\circ},
поэтому
\angle AOP=90^{\circ}-\alpha-\beta=\gamma.
Пусть прямая, проведённая через точку P
перпендикулярно AD
, пересекает прямую DE
в точке F
. Поскольку отрезок AF
виден из точек P
и O
под прямым углом, эти точки лежат на окружности с диаметром AF
. Тогда
\angle AFP=\angle AOP=\gamma,
а так как PF\parallel BO
, то
\angle PFD=\angle BOD=\alpha,
поэтому
\angle AFD=\alpha+\gamma=\angle QOE.
Значит, треугольники AFD
и QOE
подобны по двум углам.
Кроме того, подобны прямоугольные треугольники PFD
и COE
. При этом FP
и OC
— соответствующие высоты подобных треугольников AFD
и QOE
, а SC\parallel DE
. Значит,
\frac{AP}{PD}=\frac{QC}{CE}=\frac{QS}{SD},
поэтому PS\parallel AQ
, т. е. PS\parallel AC
. Отсюда следует утверждение задачи.
Аналогично для любого другого возможного случая.
Источник: Журнал «Crux Mathematicorum». — 2002, № 4, задача 2639, с. 272
