16211. Точки L
и N
— середины диагоналей соответственно AC
и BD
вписанного четырёхугольника ABCD
. Докажите, что если BD
— биссектриса угла ANC
, то AC
— биссектриса угла BLD
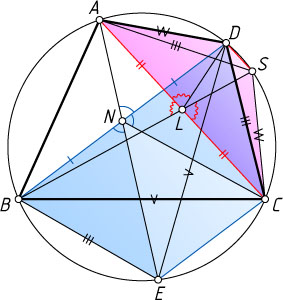
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть прямая, проведённая через точку C
параллельно диагонали BD
, вторично пересекает описанную окружность четырёхугольника ABCD
в точке E
. Тогда CEBD
— равнобедренная трапеция (или прямоугольник), поэтому BE=DC
и \angle NBE=\angle NDC
. Значит, треугольники BNE
и DNC
равны по двум сторонам и углу между ними. Тогда
\angle BNE=\angle DNC=\angle DNA.
Следовательно, точки A
, N
и E
лежат на одной прямой.
Поскольку прямая AE
проходит через середину N
диагонали BD
, высоты треугольников BAE
и DAE
с общим основанием AE
равны. Значит, эти треугольники равновелики. Тогда
\frac{1}{2}AB\cdot BE\sin\angle ABE=\frac{1}{2}AD\cdot DE\sin\angle ADE,
а так как четырёхугольник ABED
вписан в окружность, то
\angle ABE+\angle ADE=180^{\circ}~\Rightarrow~\sin\angle ABE=\sin\angle ADE.
Значит,
AB\cdot BE=AD\cdot DE.
В то же время, BE=CD
и DE=BC
, поэтому последнее равенство можно переписать в виде
AB\cdot CD=AD\cdot BC.
Пусть прямая, проведённая через точку D
параллельно диагонали AC
, вторично пересекает описанную окружность четырёхугольника ABCD
в точке S
. Тогда ASDC
— равнобедренная трапеция (или прямоугольник), поэтому AD=CS
и CD=AS
. Значит,
AB\cdot AS=CS\cdot BC,
а так как
\angle BAS+\angle BCS=180^{\circ},
то треугольники ABS
и CBS
равновелики. Тогда прямая BS
проходит через середину диагонали AC
, т. е. через точку L
, и поэтому \angle CLS=\angle ALB
.
Из параллельности DS
и AC
получаем, что AD=CS
и \angle DAL=\angle SCL
. Значит, равны треугольники ALD
и CLS
. Тогда
\angle ALD=\angle CLS=\angle ALB.
Следовательно, AC
— биссектриса угла BLD
. Что и требовалось доказать.
Аналогично для любого другого случая.
Источник: Турецкие математические олимпиады. —
Источник: Журнал «Crux Mathematicorum». — 2004, № 5, задача 2 (2002, с. 66-67), с. 274
