1622. Теорема Менелая. Дан треугольник ABC
. Точки A_{1}
и C_{1}
лежат на сторонах соответственно BC
и AB
, а точка B_{1}
— на продолжении стороны AC
за точку C
. Докажите, что точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой тогда и только тогда, когда
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Указание. Проведите через вершину B
прямую, параллельную AC
, и рассмотрите две пары образовавшихся подобных треугольников.
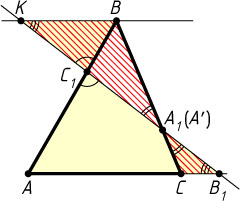
Решение. Первый способ. Пусть точки C_{1}
, A_{1}
и B_{1}
лежат на одной прямой. Через вершину B
проведём прямую, параллельную AC
. Пусть K
— точка её пересечения с прямой B_{1}C_{1}
. Из подобия треугольников BC_{1}K
и AC_{1}B_{1}
следует, что
BK=AB_{1}\cdot\frac{BC_{1}}{C_{1}A}.
Из подобия треугольников BA_{1}K
и CA_{1}B_{1}
следует, что
BK=CB_{1}\cdot\frac{BA_{1}}{A_{1}C}.
Поэтому
AB_{1}\cdot\frac{BC_{1}}{C_{1}A}=CB_{1}\cdot\frac{BA_{1}}{A_{1}C}.
Следовательно,
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1.
Обратно, пусть точки C_{1}
и A_{1}
лежат на сторонах AB
и BC
, точка B_{1}
— на продолжении стороны AC
за точку C
и при этом
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1.
Предположим, что прямая B_{1}C_{1}
пересекает сторону BC
в некоторой точке A'
. Тогда по доказанному
\frac{BA'}{A'C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1,
поэтому \frac{BA'}{A'C}=\frac{BA_{1}}{A_{1}C}
, значит, точка A'
совпадает с точкой A_{1}
. Следовательно, точки C_{1}
, A_{1}
и B_{1}
лежат на одной прямой.
Что и требовалось доказать.
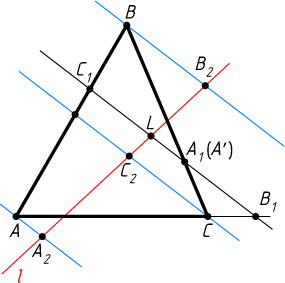
Второй способ. Пусть точки C_{1}
, A_{1}
и B_{1}
лежат на одной прямой. Проведём произвольную прямую l
, пересекающую прямую A_{1}C_{1}
в точке L
. Через точки A
, B
и C
проведём прямые, параллельные прямой A_{1}C_{1}
. Пусть A_{2}
, B_{2}
, C_{2}
— точки пересечения этих прямых с прямой l
. Тогда по теореме о пропорциональных отрезках
\frac{BA_{1}}{A_{1}C}=\frac{B_{2}L}{LC_{2}},~\frac{CB_{1}}{B_{1}A}=\frac{C_{2}L}{LA_{2}},~\frac{AC_{1}}{C_{1}B}=\frac{A_{2}L}{LB_{2}}.
Следовательно,
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=\frac{B_{2}L}{LC_{2}}\cdot\frac{C_{2}L}{LA_{2}}\cdot\frac{A_{2}L}{LB_{2}}=1.
Обратно, пусть точки C_{1}
и A_{1}
лежат на сторонах AB
и BC
, точка B_{1}
— на продолжении стороны AC
за точку C
и при этом
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1.
Предположим, что прямая B_{1}C_{1}
пересекает сторону BC
в некоторой точке A'
. Тогда по доказанному
\frac{BA'}{A'C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1,
поэтому \frac{BA'}{A'C}=\frac{BA_{1}}{A_{1}C}
, значит, точка A'
совпадает с точкой A_{1}
. Следовательно, точки C_{1}
, A_{1}
и B_{1}
лежат на одной прямой.
Что и требовалось доказать.
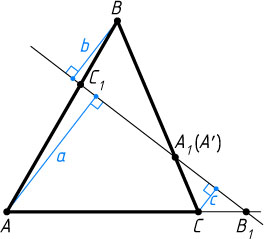
Третий способ. Пусть точки C_{1}
, A_{1}
и B_{1}
лежат на одной прямой, a
, b
и c
— высоты треугольников AB_{1}C_{1}
, BA_{1}C_{1}
и CA_{1}B_{1}
, проведённые из вершин A
, B
и C
соответственно. Тогда
\frac{BA_{1}}{A_{1}C}=\frac{b}{c},~\frac{CB_{1}}{B_{1}A}=\frac{c}{a},~\frac{AC_{1}}{C_{1}B}=\frac{a}{b}.
Следовательно,
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=\frac{b}{c}\cdot\frac{c}{a}\cdot\frac{a}{b}=1.
Обратно, пусть точки C_{1}
и A_{1}
лежат на сторонах AB
и BC
, точка B_{1}
— на продолжении стороны AC
за точку C
и при этом
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1.
Предположим, что прямая B_{1}C_{1}
пересекает сторону BC
в некоторой точке A'
. Тогда по доказанному
\frac{BA'}{A'C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1,
поэтому \frac{BA'}{A'C}=\frac{BA_{1}}{A_{1}C}
, значит, точка A'
совпадает с точкой A_{1}
. Следовательно, точки C_{1}
, A_{1}
и B_{1}
лежат на одной прямой.
Что и требовалось доказать.
Примечание. 1. Пусть \overrightarrow{AB}
и \overrightarrow{CD}
— коллинеарные векторы. Обозначим \frac{\overrightarrow{AB}}{\overrightarrow{CD}}
величину \pm\frac{AB}{CD}
, где знак плюс берётся в том случае, когда векторы \overrightarrow{AB}
и \overrightarrow{CD}
сонаправлены, а знак минус — в случае, когда векторы \overrightarrow{AB}
и \overrightarrow{CD}
противоположно направлены. Эту величину будем называть ориентированным отношением отрезков AB
и CD
.
Теорему Менелая тогда можно сформулировать так. Дан треугольник ABC
. Точки A_{1}
, B_{1}
, C_{1}
лежат на сторонах соответственно BC
, AC
и AB
(или на их продолжениях). Докажите, что точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой тогда и только тогда, когда
\frac{\overrightarrow{AB_{1}}}{\overrightarrow{B_{1}C}}\cdot\frac{\overrightarrow{CA_{1}}}{\overrightarrow{A_{1}B}}\cdot\frac{\overrightarrow{BC_{1}}}{\overrightarrow{C_{1}A}}=-1.
2. См. также статью Б.Эрдниева и Н.Манцаева: «Теоремы Чевы и Менелая», Квант, 1990, N3, с.56-59.
3. См. также статью Б.Орача: «Теорема Менелая», Квант, 1991, N3, с.52-55.
4. См. также статью А.Егорова «Теоремы Чевы и Менелая», Квант, 2004, N3, с.35-38.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 182-183
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 57(а), с. 96
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 131, с. 48
Источник: Вступительный экзамен в МФТИ. — 1951, билет 16, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 51-16-1, с. 33
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 5.58, с. 112
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.69, с. 109
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 73
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 396, с. 60
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 609
Источник: Журнал «Crux Mathematicorum». — 1977, № 1, с. 2


