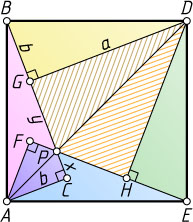
16228. Квадрат ABDE
построен на гипотенузе AB
прямоугольного треугольника ABC
, причём точка C
лежит внутри квадрата. Вершина G
треугольника BDG
, подобного треугольнику ABC
, лежит внутри квадрата ABDE
. Аналогично строятся прямоугольные треугольники EDH
и AEF
, подобные треугольнику ABC
. Пусть отрезки BC
и EF
пересекаются в точке P
. Найдите площадь четырёхугольника DGPH
, если BC=a
и AC=b
.
Ответ. \frac{a^{2}(a-b)}{a+b}
.
Решение. Все четыре прямоугольных треугольника из условия равны по гипотенузе и острому углу. В частности, BG=AC
. Пусть S
— искомая площадь четырёхугольника DGPH
.
Первый способ. Заметим, что так как отрезки BC
и EF
пересекаются, то a\gt b
. Обозначим PC=x
и PG=y
. Прямые DG
и AC
параллельны, так как обе они перпендикулярны прямой BC
. Значит, подобны прямоугольные треугольники DGP
и ACP
. Тогда
\frac{y}{x}=\frac{DG}{AC}=\frac{a}{b},
а так как
x+y=GC=BC-BG=BC-AC=a-b.
Из системы
\syst{\frac{y}{x}=\frac{a}{b}\\x+y=a-b\\}
находим, что y=\frac{a(a-b)}{a+b}
. Значит,
S_{\triangle DGP}=\frac{1}{2}DG\cdot GP=\frac{1}{2}ay=\frac{a^{2}(a-b)}{2(a+b)}.
Аналогично,
S_{\triangle DHP}=\frac{a^{2}(a-b)}{2(a+b)}.
Следовательно,
S_{DGPH}=S_{\triangle DGP}+S_{\triangle DHP}=\frac{a^{2}(a-b)}{a+b}.
Второй способ. Поскольку прямоугольные треугольники DGP
и ACP
подобны, подобны также и четырёхугольники DGPH
и ACPF
. Значит, S_{ACPF}=\frac{b^2}{a^2}S
. Площадь квадрата ABDE
равна AB^{2}=a^{2}+b^{2}
. Следовательно,
S=S_{ABDE}-4S_{\triangle ABC}+S_{ACPF},
S-\frac{b^{2}}{a^{2}}S=a^{2}+b^{2}-2ab=(a-b)^{2},
S(a^{2}-b^{2})=a^{2}(a-b)^{2},
S=\frac{a^{2}(a-b)}{a+b}.
Источник: Журнал «Crux Mathematicorum». — 2005, № 6, задача M144, с. 367
