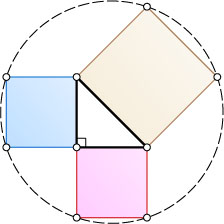
16234. На сторонах прямоугольного треугольника вне его построены три квадрата (см. рис.). Шесть вершин квадратов, не совпадающих с вершинами треугольника, лежат на одной окружности. Найдите все такие прямоугольные треугольники.
Ответ. Равнобедренные прямоугольные треугольники.
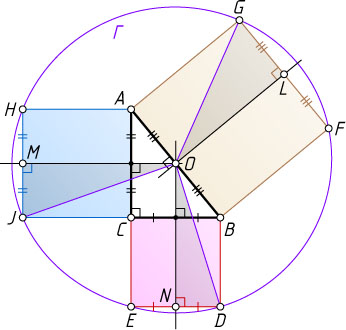
Решение. Рассмотрим прямоугольный треугольник ABC
с катетами BC=a
, AC=b
и гипотенузой AB=c
, а также окружность \Gamma
с центром O
, проходящую через шесть указанных вершин D
, E
, F
, G
, H
и J
квадратов BCED
, GFBA
и ACJH
из условия задачи. Стороны квадратов с этими вершинами являются хордами DE
, FG
и HJ
окружности \Gamma
, а серединные перпендикуляры к этим хордам совпадают с серединными перпендикулярами к соответствующим сторонам треугольника и пересекаются в точке O
. Кроме того, OJ=OD=OG
.
Пусть N
, L
и M
— середины хорд DE
, FG
и HJ
соответственно. По теореме Пифагора
OJ^{2}=OM^{2}+MJ^{2}=\left(b+\frac{a}{2}\right)^{2}+\frac{b^{2}}{4}=b^{2}+ab+\frac{1}{4}(a^{2}+b^{2}),
OD^{2}=ON^{2}+ND^{2}=\left(a+\frac{b}{2}\right)^{2}+\frac{a^{2}}{4}=a^{2}+ab+\frac{1}{4}(a^{2}+b^{2}),
OG^{2}=OL^{2}+LG^{2}=c^{2}+\frac{c^{2}}{4}=\frac{5}{4}c^{2}=\frac{5}{4}(a^{2}+b^{2})=a^{2}+b^{2}+\frac{1}{4}(a^{2}+b^{2}).
Тогда
OJ=OD=OG~\Leftrightarrow~b^{2}+ab=a^{2}+ab=a^{2}+b^{2}~\Leftrightarrow~a=b.
Следовательно, все прямоугольные треугольники, удовлетворяющие условию задачи, — равнобедренные.
Источник: Журнал «Crux Mathematicorum». — 2005, № 8, задача M152, с. 492

