16238. Для каких точек K
и L
на сторонах соответственно BC
и CD
прямоугольника ABCD
треугольники ABK
, AKL
и ADL
равновелики?
Ответ. \frac{BK}{BC}=\frac{DL}{DC}=\frac{\sqrt{5}-1}{2}
.
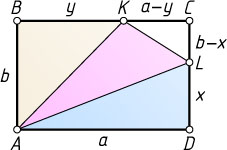
Решение. Обозначим AD=a
, AB=b
, DL=x
и BK=y
. Тогда
S_{\triangle ADL}=\frac{1}{2}ax,~S_{\triangle ABK}=\frac{1}{2}by,
S_{\triangle AKL}=ab-\frac{1}{2}ax-\frac{1}{2}by-\frac{1}{2}(a-y)(b-x)=\frac{1}{2}ab-\frac{1}{2}xy.
Поскольку по условию ax=by
и by=ab-xy
, то для некоторого t
верны равенства
\frac{x}{b}=\frac{y}{a}=t,~x=bt,~y=at~\Rightarrow~t^{2}+t-1=0,
откуда t=\frac{\sqrt{5}-1}{2}
.
Легко проверить, что верно и обратное, т. е. если t=\frac{\sqrt{5}-1}{2}
, то треугольники ABK
, AKL
и ADL
равновелики.
Источник: Бельгийские математические олимпиады. —
Источник: Журнал «Crux Mathematicorum». — 2006, № 3, задача 1 (2004, 269), с. 154
