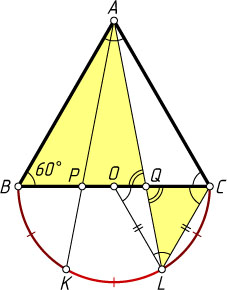
1633. На стороне BC
равностороннего треугольника ABC
как на диаметре внешним образом построена полуокружность, на которой взяты точки K
и L
, делящие полуокружность на три равные дуги. Докажите, что прямые AK
и AL
делят отрезок BC
на равные части.
Указание. Треугольники LQC
и AQB
подобны с коэффициентом \frac{1}{2}
.
Решение. Пусть O
— середина BC
, P
и Q
— точки пересечения отрезков AK
и AL
со стороной BC
(P
между B
и Q
).
Поскольку \angle LOC=\frac{180^{\circ}}{3}=60^{\circ}
и OL=OC
, то треугольник LOC
— равносторонний. Поэтому
LC=OC=\frac{1}{2}BC=\frac{1}{2}AB,~LC\parallel AB.
Из подобия треугольников LQC
и AQB
находим, что
CQ=\frac{LC}{AB}\cdot BQ=\frac{1}{2}BQ.
Следовательно, CQ=\frac{1}{3}BC
. Аналогично BP=\frac{1}{3}BC
. Таким образом, BP=PQ=QC
.
