16330. Треугольник ABC
с высотами AA'
и BB'
вписан в окружность \Gamma
. Окружность с диаметром BA'
вторично пересекает прямую BB'
в точке M
, а окружность \Gamma
— в точке P
. Докажите, что точки A
, M
и P
лежат на одной прямой.
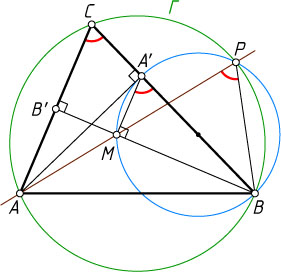
Решение. Рассмотрим случай, изображённый на рисунке.
Вписанные в окружность с диаметром BA'
углы BA'M
и BPM
опираются на одну и ту же дугу, поэтому они равны.
Поскольку \angle BMA'=90^{\circ}
, прямые MA'
и AC
параллельны, поэтому \angle BPM=\angle BCA
. В то же время, вписанные в окружность \Gamma
углы BCA
и BPA
опираются на одну дугу, значит,
\angle BPA=\angle BCA=\angle BPM.
Следовательно, точки A
, M
и P
лежат на одной прямой. Что и требовалось доказать.
Аналогично для любого другого случая.
Примечание. 1. Утверждение верно для любой точки A'
прямой BC
.
2. Рассмотрения случаев можно избежать, если рассматривать ориентированные углы.
Источник: Журнал «Crux Mathematicorum». — 2013, № 4, задача 3738 (2012, с. 150, 152), с. 197
