16337. К окружности, описанной около треугольника ABC
со сторонами BC=a
, CA=b
и AB=c
, проведена касательная. Расстояния от вершин A
, B
и C
до неё равны d_{a}
, d_{b}
и d_{c}
соответственно. Докажите, что одно из чисел a\sqrt{d_{a}}
, b\sqrt{d_{b}}
и c\sqrt{d_{c}}
равно сумме двух других.
Решение. Пусть радиус окружности равен R
, а A_{1}
, B_{1}
и C_{1}
— проекции вершин соответственно A
, B
и C
на проведённую касательную. Обозначим углы при вершинах A
, B
и C
треугольника ABC
через \alpha
, \beta
и \gamma
соответственно.
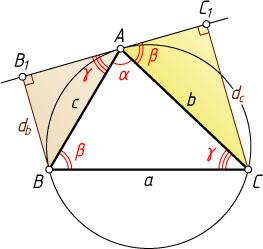
Пусть касательная проведена в точке A
(рис. 1). По теореме об угле между касательной и хордой
\angle BAB_{1}=\angle ACB=\gamma.
Тогда
\sin\gamma=\frac{BB_{1}}{AB}=\frac{d_{b}}{c}~\mbox{и}~\sin\gamma=\frac{c}{2R},
поэтому
\frac{d_{b}}{c}=\frac{c}{2R}~\Rightarrow~c^{2}=2Rd_{b}.
Аналогично, b^{2}=2Rd_{c}
. Тогда
\frac{d_{b}}{d_{c}}=\frac{c^{2}}{b^{2}}~\Rightarrow~b\sqrt{d_{b}}=c\sqrt{d_{c}},
а так как в этом случае d_{a}=0
, то верно равенство
b\sqrt{d_{b}}+a\sqrt{d_{a}}=c\sqrt{d_{c}}.
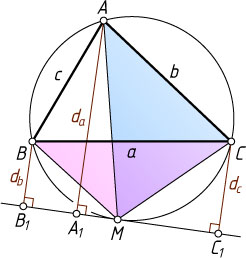
Пусть теперь касательная проведена в точке M
, отличной от вершины треугольника. Без ограничения общности будем считать, что точка M
лежит на дуге BC
, не содержащей точку A
(рис. 2).
Применив равенства, доказанные в рассмотренном выше случае, к треугольникам MBC
и MAC
, получим
MC\sqrt{d_{b}}=MB\sqrt{d_{c}}~\mbox{и}~MC\sqrt{d_{a}}=MA\sqrt{d_{c}},
поэтому
MB=\frac{MC\sqrt{d_{b}}}{\sqrt{d_{c}}}~\mbox{и}~MA=\frac{MC\sqrt{d_{a}}}{\sqrt{d_{c}}}.
По теореме Птолемея для вписанного четырёхугольника ABMC
получаем
a\cdot MA=b\cdot MB+c\cdot MC,~\mbox{или}~a\cdot\frac{MC\sqrt{d_{a}}}{\sqrt{d_{c}}}=b\cdot\frac{MC\sqrt{d_{b}}}{\sqrt{d_{c}}}+c\cdot MC.
Следовательно,
a\sqrt{d_{a}}=b\sqrt{d_{b}}+c\sqrt{d_{c}}.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2013, № 9, с. 405

