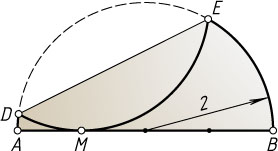
16339. Полуокружность радиуса 2 отразили симметрично относительно хорды DE
полуокружности (см. рис.). Оказалось, что отражённая дуга DE
коснулась диаметра AB
полуокружности в точке M
, причём AM:MB=1:3
. Найдите DE
.
Ответ. \sqrt{11}
.
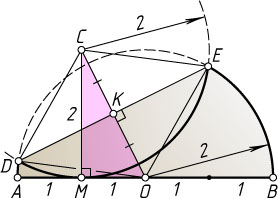
Решение. Пусть O
— центр полуокружности (середина отрезка AB
), C
— точка, симметричная точке O
относительно прямой DE
(центр окружности отражённой дуги). Тогда CM=2
, так как из симметрии отражённая дуга — это дуга окружности того же радиуса, что и данная полуокружность. Из условия задачи получаем, что OM=\frac{1}{2}OA=1
.
Из прямоугольного треугольника OMC
находим, что
OC^{2}=OM^{2}+CM^{2}=1^{2}+2^{2}=5.
Пусть K
— точка пересечения DE
и OC
. Тогда K
— точка пересечения диагоналей ромба CDOE
со стороной 2. Следовательно,
DE=2KE=2\sqrt{OE^{2}-\left(\frac{1}{2}OC\right)^{2}}=2\sqrt{4-\frac{5}{4}}=\sqrt{16-5}=\sqrt{11}.
Источник: Журнал «Crux Mathematicorum». — 2014, № 1, задача CC51, с. 5

