16353. Через точку P
, лежащую вне окружности с центром O
, проведены прямые, касающиеся окружности в точках A
и B
. Через произвольную точку M
хорды AB
перпендикулярно OM
проведена прямая, пересекающая прямые PA
и PB
в точках C
и D
. Докажите, что M
— середина отрезка CD
.
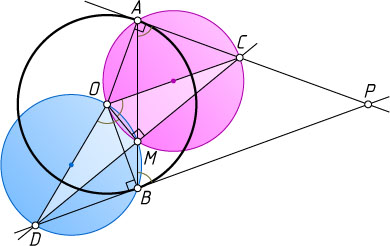
Решение. Рассмотрим случай, изображённый на рисунке. Пусть точки C
и D
лежат на прямых PA
и PB
соответственно. Из точек A
и M
отрезок OC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OC
. Аналогично, точки B
и M
лежат на окружности с диаметром OD
. Тогда
\angle COM=\angle CAM=\angle PAB=\angle PBA=180^{\circ}-\angle DBM=\angle DOM.
Прямоугольные треугольники CMO
и DMO
равны по катету и прилежащему острому углу. Следовательно, MC=MO
. Что и требовалось доказать.
Источник: Балканская математическая олимпиада. — 2014
Источник: Журнал «Crux Mathematicorum». — 2016, № 5, задача OC221, с. 204
