16361. Радиусы вписанной и описанной окружностей треугольника ABC
равны r
и R
соответственно, I
— центр вписанной окружности. Точки D
, E
и F
— центры описанных окружностей треугольников BIC
, AIC
и AIB
соответственно. Докажите, что отношение площадей треугольников DEF
и ABC
равно \frac{R}{2r}
.
Решение. Обозначим углы треугольника ABC
при вершинах A
, B
и C
через \alpha
, \beta
и \gamma
соответственно, а противолежащие им стороны — через a
, b
и c
соответственно. Пусть O
— центр описанной окружности треугольника ABC
.
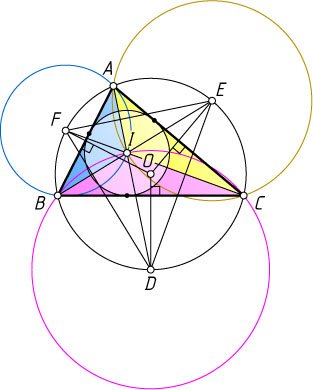
Заметим, что точки D
, E
и F
— середины не содержащих точек соответственно A
, B
и C
дуг описанной окружности треугольника ABC
(см. задачу 788), поэтому OE\perp AC
и OF\perp AB
. Значит,
\sin\angle EOF=\sin\angle BAC=\sin\alpha.
Аналогично, \sin\angle DOF=\sin\beta
и \sin\angle DOE=\sin\gamma
. Тогда
S_{\triangle DEF}=S_{\triangle EOF}+S_{\triangle DOF}+S_{\triangle DOF}=\frac{1}{2}R^{2}\sin\alpha+\frac{1}{2}R^{2}\sin\beta+\frac{1}{2}R^{2}\sin\gamma=
=\frac{1}{2}R^{2}(\sin\alpha+\sin\beta+\sin\gamma).
В то же время,
S_{\triangle ABC}=\frac{(a+b+c)r}{2}=\frac{r(2R\sin\alpha+2R\sin\beta+2R\sin\gamma)}{2}=
=rR(\sin\alpha+\sin\beta+\sin\gamma).
Следовательно,
\frac{S_{\triangle DEF}}{S_{\triangle ABC}}=\frac{\frac{1}{2}R^{2}(\sin\alpha+\sin\beta+\sin\gamma)}{rR(\sin\alpha+\sin\beta+\sin\gamma)}=\frac{R}{2r}.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2017, № 6, задача 4160, с. 273
