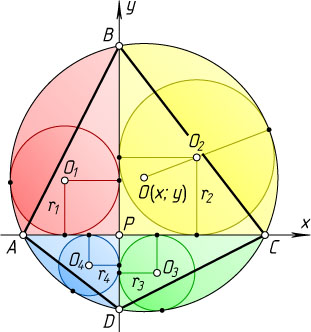
16368. Четырёхугольник ABCD
с перпендикулярными диагоналями AC
и BD
, пересекающимися в точке P
, вписан в окружность радиуса R
с центром O
. В криволинейные треугольники PAB
, PBC
, PCD
и PDA
вписаны окружности радиусов r_{1}
, r_{2}
, r_{3}
и r_{4}
соответственно. Докажите, что
r_{1}+r_{2}+r_{3}+r_{4}+8R=(R^{2}-OP^{2})\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{2}}+\frac{1}{r_{4}}\right).
Решение. Пусть O_{1}
, O_{2}
, O_{3}
и O_{4}
— центры окружностей, вписанных в криволинейные треугольники PAB
, PBC
, PCD
и PDA
соответственно.
Введём прямоугольную систему координат xPy
, направив ось Px
по лучу PC
и ось Py
по лучу PB
. Тогда расстояние между точками O_{2}(r_{2};r_{2})
и O(x;y)
равно
R-r_{2}=\sqrt{(x-r_{2})^{2}+(x-r_{2})^{2}},
причём x^{2}+y^{2}=OP^{2}
. Значит,
R-r_{2}=\sqrt{(x-r_{2})^{2}+(x-r_{2})^{2}}~\Leftrightarrow~x^{2}+y^{2}-2r_{2}(x+y)+2r_{2}^{2}=R^{2}-2Rr_{2}+r_{2}^{2}~\Leftrightarrow
\Leftrightarrow~2Rr_{2}-2r_{2}(x+y)+r_{2}^{2}=R^{2}-OP^{2}.
Следовательно,
\frac{R^{2}-OP^{2}}{r_{2}}=2R+r_{2}-2(x+y).
Аналогично,
\frac{R^{2}-OP^{2}}{r_{1}}=2R+r_{1}+2(x-y),
\frac{R^{2}-OP^{2}}{r_{3}}=2R+r_{3}+2(y-x),
\frac{R^{2}-OP^{2}}{r_{4}}=2R+r_{4}+2(x+y).
Сложив эти четыре равенства, получим
(R^{2}-OP^{2})\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{2}}+\frac{1}{r_{4}}\right)=r_{1}+r_{2}+r_{3}+r_{4}+8R
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2019, № 6, задача 4382, с. 356
