16371. Точка I
— центр вписанной окружности треугольника ABC
. Лучи AI
, BI
и CI
пересекают описанную окружность треугольника ABC
в точках M
, N
и P
соответственно. Отрезок PN
пересекает стороны AB
и AC
в точках точках E
и F
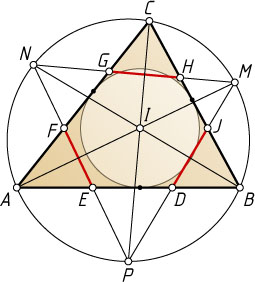
соответственно (см. рис.). Аналогично определяются точки G
, H
и точки J
, D
. Докажите, что EF=GH=JD
тогда и только тогда, когда треугольник ABC
равносторонний.
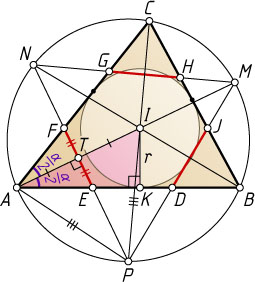
Решение. Пусть T
— точка пересечения AM
и PN
. Тогда PT\perp AI
. Поскольку PA=PI
(см. задачу 788), треугольник AIP
равнобедренный. Его высота PT
является медианой, поэтому 2AT=AI
.
Пусть радиус вписанной окружности треугольника ABC
равен r
, \angle BAC=\alpha
, а K
— проекция точки I
на прямую AB
. Тогда
EF=2ET=2\cdot AT\tg\frac{\alpha}{2}=\frac{AI\sin\frac{\alpha}{2}}{\cos\frac{\alpha}{2}}=\frac{IK}{\cos\frac{\alpha}{2}}=\frac{r}{\cos\frac{\alpha}{2}}.
Аналогично,
GH=\frac{r}{\cos\frac{\gamma}{2}},~JD=\frac{r}{\cos\frac{\beta}{2}}.
Значит,
EF=GH=JD~\Leftrightarrow~\cos\frac{\alpha}{2}=\cos\frac{\beta}{2}=\cos\frac{\gamma}{2},
а так как \frac{\alpha}{2}
, \frac{\beta}{2}
и \frac{\gamma}{2}
меньше 90^{\circ}
, то
\cos\frac{\alpha}{2}=\cos\frac{\beta}{2}=\cos\frac{\gamma}{2}~\Leftrightarrow~\frac{\alpha}{2}=\frac{\beta}{2}=\frac{\gamma}{2}~\Leftrightarrow~\alpha=\beta=\gamma.
Следовательно,
EF=GH=JD~\Leftrightarrow~\alpha=\beta=\gamma.
Отсюда получаем утверждение задачи.
Источник: Журнал «Crux Mathematicorum». — 2019, № 7, задача 4413, с. 432

