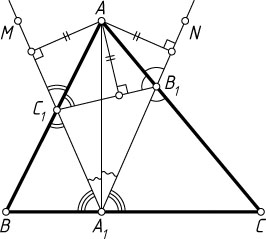
1638. На сторонах AB
, BC
и CA
остроугольного треугольника ABC
взяты точки C_{1}
, A_{1}
и B_{1}
соответственно. Докажите, что если
\angle B_{1}A_{1}C=\angle BA_{1}C_{1},~\angle A_{1}B_{1}C=\angle AB_{1}C_{1}~\mbox{и}~\angle A_{1}C_{1}B=\angle AC_{1}B_{1},
то точки A_{1}
, B_{1}
и C_{1}
являются основаниями высот треугольника ABC
.
Указание. Лучи C_{1}A
и B_{1}A
являются биссектрисами внешних углов треугольника A_{1}B_{1}C_{1}
.
Решение. На продолжении отрезка A_{1}C_{1}
за точку C_{1}
возьмём точку M
. Тогда
\angle AC_{1}M=\angle BC_{1}A_{1}=\angle AC_{1}B_{1},
т. е. C_{1}A
— биссектриса угла B_{1}C_{1}M
. Поэтому точка A
равноудалена от сторон этого угла.
Если N
— точка на продолжении A_{1}B_{1}
за точку B_{1}
, то аналогично докажем, что точка A
равноудалена от сторон угла NB_{1}C_{1}
. Следовательно, точка A
равноудалена от сторон угла MA_{1}N
, т. е. лежит на биссектрисе этого угла. Поэтому
\angle AA_{1}C=\angle AA_{1}B_{1}+\angle B_{1}A_{1}C=\angle AA_{1}C_{1}+\angle C_{1}A_{1}B=\angle AA_{1}B.
Следовательно, AA_{1}\perp BC
.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.57(б), с. 17
Источник: Всесибирская физико-математическая олимпиада. — 2011, заключительный этап, задача 4, 10 класс
