16406. Точка P
лежит вне окружности с центром O
. Прямая, проходящая через точку P
, пересекает окружность в точках A
и B
. Касательные к окружности, проведённые в этих точках, пересекают прямую, проходящую через точку P
перпендикулярно OP
, в точках C
и D
. Верно ли, что PC=PD
?
Ответ. Верно.
Решение. Из точек B
и P
отрезок OC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OC
. Аналогично, точки A
и P
лежат на окружности с диаметром OD
. Тогда
\angle BCO=\angle BPO=\angle APO=\angle ADO.
Прямоугольные треугольники CBO
и DAO
равны по катету (OB=OA
) и противолежащему острому углу, поэтому OC=OD
. Значит, OP
— серединный перпендикуляр к отрезку CD
. Следовательно, PC=PD
.
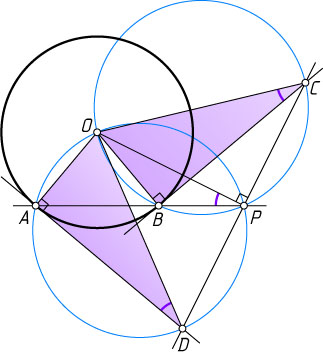
Источник: Журнал «Mathematics Magazine». — 1934, том 8, № 7, задача 53, с. 170
