16444. На стороне AB
единичного квадрата ABCD
отмечена точка E
на расстоянии AE=\frac{1}{r}
. Постройте на стороне AB
точку F
на расстоянии \frac{1}{r+1}
от точки A
.
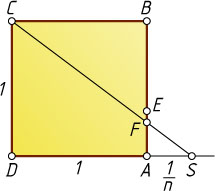
Решение. На продолжении стороны AD
за точку A
отложим отрезок AS=AE=\frac{1}{r}
. Тогда отрезок CS
пересекает сторону AB
в искомой точке F
.
Действительно, из подобия треугольников AFS
и DCS
получаем
\frac{AF}{DC}=\frac{SA}{SD}=\frac{SA}{SA+SD}=\frac{\frac{1}{r}}{\frac{1}{r}+1}=\frac{1}{r+1}.
Следовательно,
AF=DC\cdot\frac{1}{r+1}=\frac{1}{r+1}.
Источник: Журнал «Mathematics Magazine». — 1956, том 29, № 5, задача 252, с. 285
