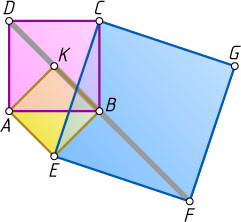
16448. На рисунке изображены три одинаково ориентированных квадрата ABCD
, AEBK
и CEFG
. Докажите, что B
— середина отрезка DF
.
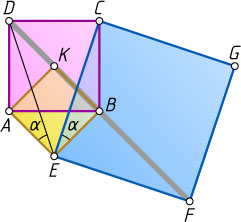
Решение. Обозначим \angle BEC=\angle AED=\alpha
. Тогда
\angle BED=\angle BEA-\alpha=90^{\circ}-\alpha=\angle FEC-\alpha=\angle FEB.
Кроме того, DE=EC=EF
. Значит, треугольники BED
и BEF
с общей стороной BE
равны по двум сторонам и углу между ними. Следовательно, BD=BF
, а так как
\angle EBF=\angle EBD=\angle EBA+\angle DBA=45^{\circ}+45^{\circ}=90^{\circ},
то точки D
, B
и F
лежат на одной прямой. Отсюда получаем утверждение задачи.
Источник: Журнал «Mathematics Magazine». — 1959, том 32, № 4, задача 349, с. 223

