1645. Биссектриса внешнего угла A
треугольника ABC
пересекает продолжение стороны BC
и точке M
. Докажите, что \frac{BM}{MC}=\frac{AB}{AC}
.
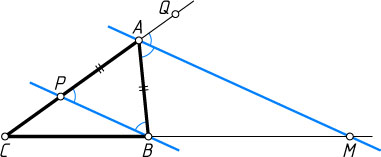
Решение. Через вершину B
проведём прямую, параллельную AM
. Пусть эта прямая пересекает сторону AC
в точке P
. Отметим точку Q
на продолжении стороны AC
за точку A
. Тогда
\angle APB=\angle QAM=\angle MAB=\angle ABP,
значит, треугольник APB
— равнобедренный, PA=AB
.
Из теоремы о пропорциональных отрезках следует, что
\frac{BM}{MC}=\frac{PA}{AC}=\frac{AB}{AC}.
Примечание. Верно и обратное: если точка M
лежит на продолжении стороны BC
треугольника ABC
и при этом \frac{BM}{MC}=\frac{AB}{AC}
, то AM
— биссектриса внешнего угла треугольника ABC
при вершине A
.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 114
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 47, с. 77
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 9, с. 7
