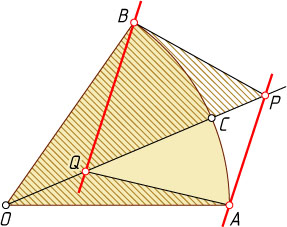
16486. Точка C
лежит на дуге сектора AOB
окружности с центром O
(см. рис.). Через точки A
и B
проведены параллельные прямые, пересекающие луч OC
в точках P
и Q
соответственно. Докажите, что площадь пятиугольника OAQPB
не зависит от выбора точки C
и параллельных прямых AP
и BQ
.
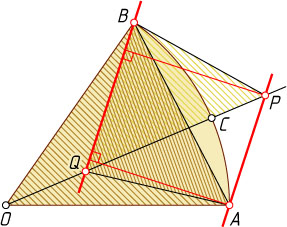
Решение. Докажем что при любом выборе точки C
и параллельных прямых AP
и BQ
из условия задачи площадь пятиугольника OAQPB
равна площади треугольника AOB
. Без ограничения общности будем считать, что точка Q
расположена ближе к O
, чем P
, т. е. точка Q
лежит внутри треугольника AOB
.
Действительно, треугольники BQP
и BQA
равновелики, так как BQ
— их общее основание, а из-за параллельности AP
и BQ
равны проведённые к нему высоты.
Источник: Журнал «Mathematics Magazine». — 1992, том 65, № 3, задача Q793, с. 195 и 200

