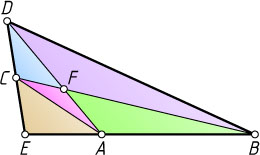
16493. В треугольнике EDB
(см. рис.) точки A
и C
лежат на сторонах BE
и DE
соответственно, а отрезки DA
и BC
пересекаются в точке S
. Известно, что
\frac{S_{\triangle EDB}}{S_{\triangle ECA}}=6,~DC\cdot AB=4~\mbox{и}~S_{\triangle CFA}+S_{\triangle DFB}=\frac{14}{5}.
Докажите, что треугольник DEB
прямоугольный.
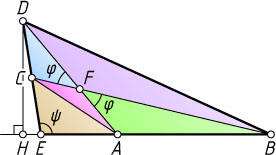
Решение. Применив теорему Менелая к треугольнику ADE
и прямой BC
, а также к треугольнику BCE
и прямой AD
, получим
\frac{DC}{CE}\cdot\frac{EB}{BA}\cdot\frac{AF}{FD}=1~\mbox{и}~\frac{BA}{AE}\cdot\frac{ED}{DC}\cdot\frac{CF}{FB}=1,
откуда
\frac{FD}{AF}=\frac{DC}{CE}\cdot\frac{EB}{BA}~\mbox{и}~\frac{FB}{CF}=\frac{BA}{AE}\cdot\frac{ED}{DC}=1.
Обозначим \angle AFB=\angle DFC=\varphi
. Тогда
\frac{S_{\triangle DFB}}{S_{\triangle CFA}}=\frac{\frac{1}{2}DF\cdot FB\sin\varphi}{\frac{1}{2}AF\cdot CF\sin\varphi}=\frac{DF}{AF}\cdot\frac{FB}{CF}=\left(\frac{DC}{CE}\cdot\frac{EB}{BA}\right)\left(\frac{BA}{AE}\cdot\frac{ED}{DC}\right)=
=\frac{EB\cdot ED}{CE\cdot AE}=\frac{\frac{1}{2}EB\cdot ED\sin\varphi}{\frac{1}{2}CE\cdot AE\sin\varphi}=\frac{S_{\triangle EDB}}{S_{\triangle ECA}}.
Таким образом,
\frac{S_{\triangle DFB}}{S_{\triangle CFA}}=\frac{S_{\triangle EDB}}{S_{\triangle ECA}}.
Обозначим \angle BED=\psi
. Пусть DH
— высота треугольника DEB
. Тогда
S_{\triangle DFB}+S_{\triangle FAB}=S_{\triangle DAB}=\frac{1}{2}AB\cdot DH=\frac{1}{2}AB\cdot DE\sin\psi.
Аналогично,
S_{\triangle CFA}+S_{\triangle FAB}=S_{\triangle DAB}=\frac{1}{2}AB\cdot CE\sin\psi.
Тогда
S_{\triangle DFB}-S_{\triangle CFA}=\frac{1}{2}AB(DE-CE)\sin\psi=\frac{1}{2}AB\cdot DC\sin\psi,
а так как
\frac{S_{\triangle DFB}}{S_{\triangle CFA}}=\frac{S_{\triangle EDB}}{S_{\triangle ECA}}=6,
а по условию
S_{\triangle CFA}+S_{\triangle DFB}=\frac{14}{5}
то
S_{\triangle CFA}=\frac{2}{5}~\mbox{и}~S_{\triangle DFB}=\frac{12}{5}.
Тогда
\frac{1}{2}AB\cdot DC\sin\psi=S_{\triangle DFB}-S_{\triangle CFA}=\frac{12}{5}-\frac{2}{5}=2,
а так как по условию AB\cdot DC=4
, то \frac{1}{2}\cdot4\sin\psi=2
. Следовательно, \sin\psi=1
, и \psi=90^{\circ}
. Что и требовалось доказать.
Источник: Журнал «Mathematics Magazine». — 1996, том 69, № 2, задача 1469, с. 144

